مدل سازی آکوستیک شبیه سازی و نحوه محاسبه نیروی تابش صوتی ،نیروی تابش صوتی یک پدیده صوتی غیرخطی مهم است که خود را به عنوان نیروی غیر صفر اعمال شده توسط میدان های صوتی بر ذرات نشان می دهد. تابش آکوستیک یک پدیده آکوستوفورتیک است، یعنی حرکت اجسام توسط صوت. یکی از نمونه های جالب این نیرو در عمل، حرکت ذرات صوتی است که در این پست وبلاگ قبلی مورد بحث قرار گرفت. امروز، ماهیت این نیرو را بررسی خواهیم کرد و نشان خواهیم داد که چگونه می توان آن را با استفاده از COMSOL Multiphysics کامسول محاسبه کرد.
نیروی تشعشع صوتی چیست و چگونه کار می کند
برای درک ماهیت نیروی تابش صوتی، اجازه دهید ابتدا یک مثال ساده از یک ذره در یک میدان فشار موج ایستاده را در نظر بگیریم (در اینجا فرض میشود که بدون تلفات است).
نیروی وارد بر ذره در نتیجه اندازه محدود ذره ایجاد می شود، به طوری که گرادیان های میدان فشار باعث می شود نیروی بیشتری به یک طرف ذره نسبت به طرف دیگر وارد شود. با این حال، اگر یک موج فشار هارمونیک را در نظر بگیریم، انتظار می رود که نیرو به عنوان یک تابع هارمونیک رفتار کند که می تواند به صورت . من این را به صورت یک فلش سیاه در انیمیشن زیر نشان داده ام.
استخراج معادلات آکوستیک
ما متوجه خواهیم شد که آنها از معادلات ناویر-استوکس در نتیجه یک روش خطی سازی پدید می آیند که معمولاً در دو مرحله انجام می شود.

اول، یک اغتشاش بسیار کوچک متغیر با زمان در فشار و سرعت در بالای یک میدان پسزمینه ثابت فرض میشود. هنگامی که مشتقات زمانی اعمال میشوند، عبارتهای ثابت حذف میشوند و آنچه باقی میماند فقط شامل شرایط اغتشاش وابسته به زمان میشود. عبارت باقیمانده شامل سهم خطی و غیرخطی خواهد بود. دومی به شکل محصولات دو یا چند ترم اغتشاش خطی ظاهر میشود و از جملههای همرفتی و اینرسی در معادله اصلی ناویر-استوکس حاصل میشود.

اما در سادهترین حد آکوستیک، سهم عبارتهای غیرخطی را میتوان نادیده گرفت زیرا دامنه اختلالات در نظر گرفته شده بسیار کوچک است. به عنوان مثال، 0.012 بسیار کوچکتر از 0.01 است و بنابراین می توان از آن صرف نظر کرد. بنابراین در مرحله دوم از روش خطی سازی، از تمام اصطلاحات غیرخطی صرف نظر شده و معادله موج خطی به دست می آید.
![]()
آنچه کینگ اشاره کرده است این است که برای درک و ارزیابی اثر نیروی تشعشع صوتی، اصطلاحات غیرخطی باید به نحوی در معادلات حفظ شوند.
با حفظ عبارات تا مرتبه دوم، میدان فشار به صورت ترکیبی از دو عبارت ظاهر میشود، که در آن و میتوان آن را به شکلی ساده بیان کرد، که به عنوان تابعی خطی از سرعت اغتشاش ظاهر میشود، و به صورت غیرخطی ظاهر میشود. عملکرد . از آنجایی که در حد آکوستیک فقط مواردی را در نظر می گیریم که سرعت آدیاباتیک صوت کجاست، نتیجه می گیریم که .
در این مرحله، ما آماده پاسخ به اولین سوال هستیم: نیروی تابش صوتی از کجا می آید؟

با بازگشت به مثال یک ذره در یک میدان فشار موج ایستاده، اجازه دهید اجزای خطی و غیرخطی فشار و نیروهای تولید شده توسط این اجزا را بررسی کنیم. در این حالت، یک تابع زمان هارمونیک خواهد بود و یک تابع ضد هارمونیک ناشی از سهم غیر خطی خواهد بود.
این اصطلاحات با شکل موج در انیمیشن بالا تجسم می شوند. نیروهای حاصل از این شرایط فشار با فلش نشان داده می شوند. نیروی خطی (فلش سیاه) هم در قدر و هم جهت تغییر می کند، بنابراین سهم متوسط چرخه آن صفر است، در حالی که عبارت غیر خطی (فلش قرمز) فقط در قدر تغییر می کند و به طور متوسط نیروی غیر صفر اعمال می کند.
محاسبه نیروی تابش صوتی
تجزیه و تحلیل ساده بالا مکانیسم اصلی پدیده نیروی تابش صوتی را نشان می دهد. به طور شهودی، متوجه می شویم که اگر ذره دارای خواص صوتی مشابه محیط اطراف باشد، هیچ نیرویی ظاهر نمی شود. به عبارت دیگر، نیروی تابش نه تنها باید تابعی از اندازه یک ذره و دامنه میدان صوتی، بلکه تابعی از کنتراست صوتی ذره (نسبت خواص ماده ذره نسبت به سیال اطراف) باشد. .
به دلیل کنتراست صوتی، برخورد میدانی روی ذره از سطح آن منعکس میشود و نیروی تابش حاصل ترکیبی از امواج فرود و منعکس شده خواهد بود. این مسئله حل تحلیلی مشکل را بسیار دشوار می کند. راه حل در یک فرم تحلیلی بسته تنها برای برخی موارد محدود توسط تعدادی از نویسندگان ارائه شد، که از کینگ شروع شد. او ذرات کروی صلب را با ابعاد بسیار کوچکتر از طول موج موج فرودی، اما بسیار بزرگتر از عمق لزج و حرارت پوست در نظر گرفته است. این دومین فرضی بود که اجازه داد این اصطلاحات نادیده گرفته شوند.
نتایج کینگ برای شامل ذرات تراکم پذیر مانند “فشار تابش صوتی بر روی یک کره تراکم پذیر” گسترش یافته است. نتایج این مطالعه بعداً توسط ال.
در یک میدان صوتی در یک سیال ایده آل. اثرات چسبناک و حرارتی زمانی اهمیت پیدا میکنند که اندازه ذرات با لایههای مرزی آکوستیک (حرارتی و چسبناک) قابل مقایسه باشد. نتایج از جمله ویسکوزیته اخیراً در سال 2012 توسط M. Settnes و H. Bruus ارائه شد.
پیاده سازی روش حل اغتشاش در مولتی فیزیک COMSOL
به طور کلی، تمام نیروها را می توان با استفاده از شارهای تکانه بیان کرد، که در آن سطح ادغام، سطح خارجی ذره است.
گورکوف از این واقعیت برای به دست آوردن یک بیان تحلیلی شکل بسته برای نیرویی که بر یک ذره در یک میدان صوتی دلخواه عمل می کند استفاده کرده است. برای محاسبه نیروی تابش آکوستیک غیرخطی، شار تکانه ناشی از میدان صوتی باید تا ترم های مرتبه دوم ارزیابی شود. جذابیت اصلی نتیجه او این است که، همانطور که قبلا ذکر شد، اصطلاحات مرتبه دوم را می توان با استفاده از حل یک مسئله خطی بیان کرد.
برای اجرای روش او، تنها کاری که ما باید انجام دهیم این است که مسئله آکوستیک را حل کنیم، از نتایج برای محاسبه شار حرکت مرتبه دوم استفاده کنیم و راه حل را با انتگرال شار جایگزین کنیم.
-
Bruus نشان داده است که با غفلت از اثرات ترموویسکوز، اصطلاحات شار مرتبه دوم عبارتند از:
انتگرال باید روی سطح یک ذره که در پاسخ به نیروی اعمال شده حرکت می کند گرفته شود. این بدان معناست که سطح ادغام تابعی از زمان است. برای غلبه بر این مشکل، یوسیکا و کاواسیما نشان دادهاند که ادغام میتواند به سطح تعادلی تبدیل شود که ذره را در بر میگیرد. با جبران خطا با اضافه کردن یک شار حرکت همرفتی، نیرو در مجموع به صورت زیر در میآید:
اکنون تنها کاری که باید انجام شود حل مسئله آکوستیک برای بدست آوردن فشار و سرعت آکوستیک و جایگزینی آنها به انتگرال در معادله است. (5). برخلاف رویکرد مورد استفاده در معادله (1) تا (3)، بیان نیرو در معادله. (5) تا زمانی که تنش داده شود برای همه اندازه ذرات معتبر است. این رویکرد اخیراً توسط گروهی از محققان دانشگاه ساوتهمپتون در COMSOL Multiphysics پیاده سازی شده است.
لازم به ذکر است که عبارت در معادله (4) تنها زمانی صادق است که اثرات چسبناک و حرارتی نادیده گرفته شوند. اگر این تلفات گنجانده شود، سطح ادغام باید خارج از لایه های مرزی گرفته شود یا یک بیان تنش کامل صحیح برای استفاده در سطح ذرات باشد. اولین رویکرد اغتشاش اصلی شامل تلفات حرارتی و ویسکوزیته در کنفرانس ICA-ASA 2013 توسط M. J. Herring Jensen و H. Bruus با عنوان “شبیه سازی اصل اول نیروی تابش صوتی بر روی ریز ذرات در امواج ایستاده اولتراسونیک” ارائه شد. مشتق دقیق معادلات حاکم تا مرتبه دوم، به شکلی که برای پیاده سازی در COMSOL Multiphysics مناسب است، در مقاله «مطالعه عددی اثرات ترموویسکوز در جریان آکوستیک ناشی از فراصوت در میکروکانال ها» ارائه شده است.
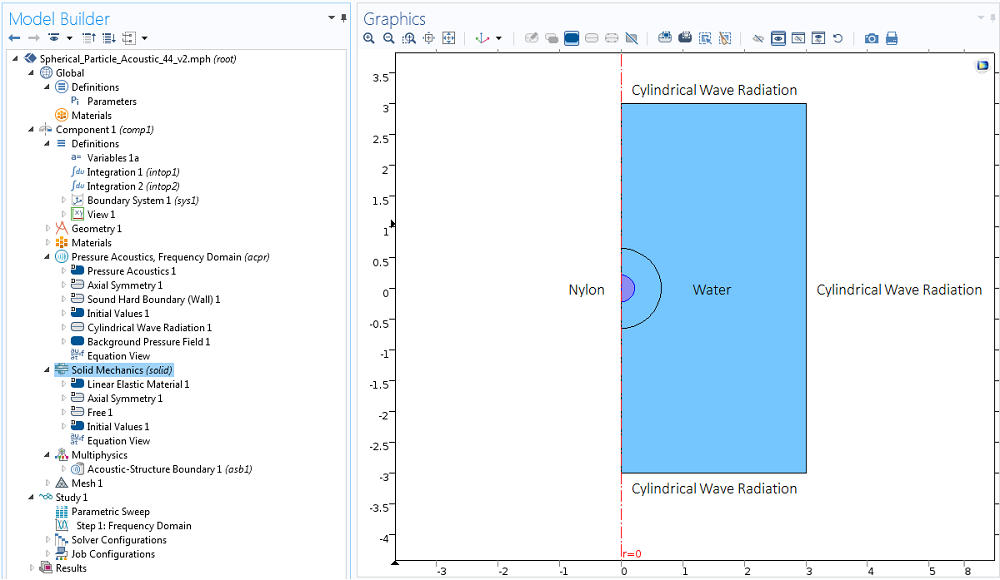
برای محک زدن روش ارائه شده توسط گلین جونز و همکاران، بیایید یک نیروی تابش صوتی اعمال شده توسط یک موج ایستاده بر روی یک ذره نایلونی کروی غوطه ور در آب را محاسبه کنیم. فرکانس 1 مگاهرتز و دامنه فشار 1 بار را فرض می کنیم و مدل را با استفاده از رابط تعاملی سازه-آکوستیک در هندسه متقارن محوری دوبعدی پیاده سازی می کنیم. اندازه جعبه در مدل چهار طول موج بلند و دو طول موج عرض است.
در اینجا قابل ذکر است که محاسبات نیروی مورد استفاده در این روش به دلیل اینکه شار در خارج از ذره قرار دارد، مستقل از سطح ادغام است. در واقع، استفاده از یک سطح در فواصل بزرگتر از نظر عددی دقیق تر خواهد بود، فقط به این دلیل که نقاط بیشتری برای ارزیابی عددی انتگرال وجود دارد. برای انجام این ادغام، میتوانیم سطح خارجی دیگری به ذره اضافه کنیم.
مقایسه نتایج با یک راه حل تحلیلی
ما اکنون آماده هستیم تا رویکرد اغتشاش را با یک راه حل تحلیلی مقایسه کنیم.
همانطور که انتظار می رود، آنها به خوبی برای شعاع ذرات کوچک که در آن راه حل تحلیلی در نظر گرفته شده معتبر است، مقایسه می شوند. برخی از مدلهای تحلیلی که شامل هارمونیکهای بالاتر در تجزیه میدان پراکنده میشوند، راهحلهایی ارائه میدهند که با رویکرد عددی مشخص شده برای ذرات کروی بزرگ و کوچک مطابقت دارد.