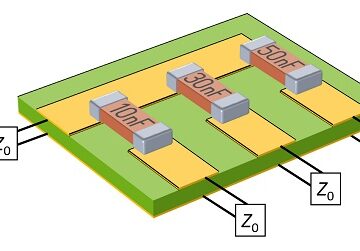
شبیه سازی پروژه اپتیک فرانهوفر کامسول
شبیه سازی پروژه اپتیک فرانهوفر کامسول ابتدا، اجازه دهید اصطلاحات و تعریف را روشن کنیم. سه عبارت برای تشخیص وجود دارد: تبدیل فوریه (FT)، تبدیل فوریه گسسته (DFT) و FFT. FT یک تابع به صورت تعریف می شود
که و به ترتیب در فضای فیزیکی و فضای فوریه متغیر هستند. زمانی که متغیر فضای فیزیکی زمان باشد، به متغیر فرکانس گفته می شود. در اپتیک به فرکانس فضایی اطلاق می شود که معمولاً با طول موج و فاصله کانونی مقیاس می شود (ما بعداً در مورد آن بحث خواهیم کرد)، در حالی که مختصات فضای فیزیکی است که برای توصیف مکان در مجاورت ساختار نوری مورد نظر استفاده می شود.
آموزش کامسول شبیه سازی پروژه اپتیک فرانهوفر کامسول
در پستهای وبلاگ قبلی، «نحوه پیادهسازی تبدیل فوریه در COMSOL Multiphysics» و «نحوه پیادهسازی تبدیل فوریه از راهحلهای محاسبهشده»، درباره نحوه انجام FT در COMSOL بحث کردیم. ما می توانیم از یک تکنیک عددی استفاده کنیم که فرمول تبدیل فوریه را به صورت مستقیم انجام می دهد.

ادغام عددی بر اساس قانون سیمپسون. ممکن است بعداً در این پست وبلاگ آن را “FT با ادغام عددی” بنامیم.
DFT نسخه گسسته FT است که عملیات را روی مجموعه ای از نقاط مجزا انجام می دهد. در COMSOL، به این صورت تعریف شده است
FFT یک الگوریتم کارآمد است که DFT را محاسبه می کند.
توجه داشته باشید که این تعاریف برای FT و DFT کلیترین تعاریف هستند، اما قرارداد علامت با قرارداد علامت COMSOL برای فرمولبندی موج سازگار نیست. هنگامی که از آن برای فرمول های پراش فراونهوفر و فرنل استفاده می کنیم، آگاهانه از این تعریف استاندارد با احتیاط استفاده می کنیم. ناهماهنگی بر راه حل های ثابت تأثیر نمی گذارد.
نحوه استفاده از ویژگی فضایی FFT
بیایید نحوه استفاده از ویژگی جدید فضایی FFT در COMSOL برای اپتیک را نشان دهیم. ویژگی FFT را می توان به ترتیب با استفاده از مراحل 1 و 2 تنظیم و اجرا کرد:
مرحله 1: مجموعه داده را آماده کنید.
با کلیک راست روی Datasets → More Datasets یک مجموعه داده فضایی FFT اضافه کنید (این فضای فوریه را مشخص می کند)
تابع مستطیلی یکی از پرکاربردترین توابع در اپتیک است زیرا نشان دهنده دیافراگم سخت است.
هنگامی که دیافراگم سخت وجود دارد، FT تابع مستطیلی همیشه درگیر است. تبدیل فوریه تابع مستطیل را می توان به راحتی با دست محاسبه کرد و به صورت زیر شناخته می شود:
جایی که مخفف عملگر تبدیل فوریه است، یک ثابت است و تابع sinc است.
بیایید نگاهی به نحوه محاسبه این FT با ویژگی جدید Spatial FFT در COMSOL بیندازیم.
تابع مستطیلی یک تابع داخلی در زیر تعریف > توابع است.
مقالات بخش آموزش comsol در حوره اپتیک
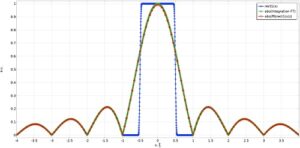
با فشار دادن دکمه Create Plot، مجموعه داده جدیدی برای تابع به طور خودکار در زیر گره Datasets در زیر Results ایجاد می شود. محدوده و وضوح نیز به طور خودکار به طور پیش فرض تنظیم می شوند. هنگام انجام FFT، مهم است که خودتان این پارامترها را کنترل کنید. وضوح فضای فوریه توسط متقابل محدوده فضای فیزیکی و لایه صفر به داده های فضای فیزیکی تعیین می شود. محدوده فضای فوریه با محدوده فضای فیزیکی و عدد نمونه برداری فضای فوریه تعیین می شود. بزرگی نتایج FFT بر اساس محدوده فضای فیزیکی و عدد نمونه برداری از فضای فوریه متفاوت است. جدول زیر خلاصه ای از عبارات پارامتر FFT، شامل مقادیر پارامتری است که مطابق با تنظیمات FFT نشان داده شده در تصویر قبلی است. با تنظیمات فوق، نمودارهای زیر تابع مستطیل شکل، rect1(x) و مقدار مطلق هستند. آن
FT، abs(fft(rect1(x))، با ویژگی FFT محاسبه می شود. محدوده کل فضای فوریه = 16/2 = 8 است، یعنی از 4- تا 4. می توانید ببینید که تعداد کل نقاط نمونه برداری در فضای فوریه = 32 است. میتونید مطالعه کنید در مورد هایپرترمی اثرات بیولوژیکی گرما در درمان سرطان کامسول از مقاله قبلی است.
چرا ؟ به این دلیل است که در لایه صفر، صفرها به دو طرف داده های فضای فیزیکی اضافه می شوند. وضوح فضای فوریه 8/32 = 0.25 است. بدون نرمال سازی، عملیات FFT منجر به فاکتور . بنابراین، باید نتایج را در ضرب کنیم تا یک مقدار پیک واحد بدست آوریم. بعداً از FFT برای فرمول های مختلف استفاده خواهیم کرد که هر کدام ثابت ضرب متفاوتی دارند. به همین دلیل، ما باید نتیجه FFT را به وحدت عادی تبدیل کنیم.
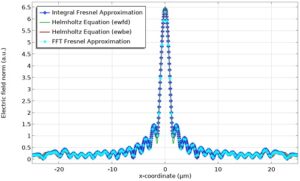
تبدیل فوریه در اپتیک
تا اینجا نحوه تنظیم و استفاده از ویژگی Spatial FFT برای یک تابع مستطیلی که یک تابع تحلیلی 1 بعدی است را یاد گرفتیم. حال بیایید از آن برای چند مثال کاربردی کاربردی در اپتیک استفاده کنیم.
در اپتیک، تبدیل فوریه فرکانس Fraunhofer زمان، که سیگنال زمانی میدان الکتریکی نور را به طیف های آن مرتبط می کند.