شبیه سازی میکرو آنتن با کامسول

شبیه سازی میکرو آنتن با کامسول عنصر کرل که گاهی اوقات عنصر لبه یا عنصر برداری نامیده می شود، به طور گسترده در روش اجزای محدود برای حل مسائل الکترومغناطیسی استفاده می شود. این پست وبلاگ یک معرفی جامع از این نوع عنصر، از جمله چرایی و چگونگی استفاده از آن در نرم افزار COMSOL  ارائه می دهد. درک چرایی و چگونگی استفاده از عنصر کرل، با این حال، ساده نیست. بنابراین، ابتدا به بررسی برخی اطلاعات پیش زمینه در مورد معادلات ماکسول و روش اجزای محدود می پردازیم.

آموزش کامسول معادلات قابل حل در الکترومغناطیسی

هدف از مدلسازی الکترومغناطیسی حل معادلات ماکسول تحت شرایط مرزی معین است.
شدت میدان الکتریکی و مغناطیسی به ترتیب کجا و هستند. و به ترتیب میدان جابجایی الکتریکی و چگالی شار مغناطیسی هستند. و و به ترتیب چگالی بار الکتریکی و چگالی جریان هدایت الکتریکی هستند.

برای به دست آوردن یک سیستم بسته، معادله ماکسول شامل روابط سازنده ای است که خواص ماکروسکوپی محیط را توصیف می کند. با آموزش COMSOL ، می‌توانید طیف وسیعی از محیط‌های مختلف، از جمله مواد غیرخطی و ناهمسانگرد را مدل‌سازی کنید. با این حال، برای سادگی، از اثر باقیمانده غفلت می‌کنیم و محیط را خطی و همسانگرد فرض می‌کنیم، که در نتیجه یک رابطه سازنده ساده ارائه می‌شود.
معادلات (7) و (8) بیانگر این است که میدان الکتریکی مماسی و جزء نرمال میدان شار مغناطیسی در مرز پیوسته هستند، در حالی که معادله (6) و (9) دلالت دارند که جزء طبیعی میدان شار الکتریکی و میدان مغناطیسی مماسی می توانند ناپیوسته باشند.

برای مسائل خاص، حل زیرمجموعه ها یا موارد خاص معادلات ماکسول همیشه راحت است که منجر به فرمول های الکتریکی، مغناطیسی یا الکترومغناطیسی متفاوت می شود. بر اساس این فرمول‌بندی‌ها، COMSOL  چندین ماژول الکترومغناطیسی (به عنوان مثال، ماژول AC/DC، ماژول RF و ماژول اپتیک موج) و همچنین چندین رابط فیزیک مختلف برای هر ماژول دارد.

به عنوان مثال، رابط الکترواستاتیک در ماژول AC/DC، مشکلات الکترواستاتیکی را که فقط بار استاتیکی وجود دارد، مدل می‌کند. توابع شکل و عناصر لاگرانژ
در COMSOL Multiphysics، روش اجزای محدود (FEM) به طور کلی برای حل معادلات دیفرانسیل جزئی (PDEs) استفاده می شود و معادلات ماکسول نیز از این قاعده مستثنی نیستند. روش اجزای محدود برای حل PDE ها در چندین مرحله استفاده می شود، از جمله:

دامنه را به بسیاری از عناصر کوچک و بدون همپوشانی تقسیم کنید که به آنها عناصر مش می گویند.
راه حل در هر عنصر با یک تابع شکل محلی یا تابع پایه تقریب می شود.
PDE ها را به شکل ضعیف بنویسید، روی هر عنصر مش گسسته کنید تا ماتریس های محلی به دست آید.

ماتریس های محلی را در یک ماتریس سراسری جمع آوری کنید و آن را حل کنید.
اجازه دهید معادله پواسون (10) را به عنوان مثال در نظر بگیریم تا نحوه عملکرد FEM را نشان دهیم. بسته به تابع شکل مورد استفاده می توانیم از عناصر مختلفی استفاده کنیم. برای سادگی، دامنه را دوبعدی در نظر می گیریم و از یک عنصر لاگرانژ مثلثی خطی استفاده می کنیم. از آن می بینیم که هر راس درجه آزادی (DOF) اضافه می کند و تابع شکل مربوطه برابر با یک در راس است اما صفر است. در تمام رئوس دیگر عنصر لاگرانژ مرتبه بالاتر، DOFها را نه تنها روی راس‌ها، بلکه به گره‌های دیگری که در عنصر قرار دارند اضافه می‌کند. بنابراین عنصر لاگرانژ عنصر گرهی نیز نامیده می شود. توابع شکل یک عنصر لاگرانژ مثلثی خطی در زیر نمایش داده شده است. برای دانستن بیشتر میتوانید برای آموزش comsol اقدام کنید.
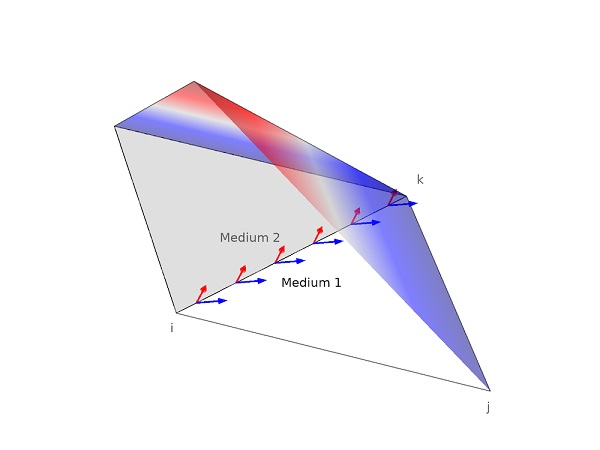
همچنین می توان از FEM مبتنی بر عنصر لاگرانژ برای حل معادله برداری (12) با تقسیم آن به اجزای مختلف استفاده کرد. با این حال، اجرای شرایط مرزی، به ویژه برای مرزهای نامنظم، پیچیده است. با این حال، نتایج می‌توانند جعلی باشند، زیرا عنصر لاگرانژ هر جزء را مجبور می‌کند تا در سراسر مرز پیوسته باشد، که این واقعیت را نقض می‌کند که جزء طبیعی میدان الکتریکی می‌تواند در رابط‌های مواد، به‌ویژه در مرزهای گوشه‌های تیز، ناپیوسته باشد.

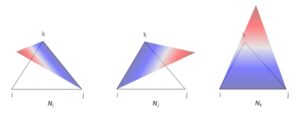
معایب عنصر کرل و شبیه سازی میکرو آنتن با کامسول

ما نشان دادیم که با استفاده از عناصر حلقه، شرایط مرزی معادلات ماکسول را می توان به طور طبیعی مدیریت کرد. عناصر حلقه، میدان الکتریکی مماسی را مجبور می‌کنند که پیوسته باشد و به میدان الکتریکی عادی اجازه می‌دهد تا از مرزها بپرد. علاوه بر این، محدود کردن سایر شرایط مرزی را آسان تر می کند. اگر غلاقه مند به مباحث شبیه سازی میکرو اسپیکر با کامسول هستید مطالعه کنید.

در این پست وبلاگ، با شروع معادلات ماکسول و شرایط مرزی آنها، دو نوع اصلی از معادلات را که اغلب در مدل‌سازی الکترومغناطیسی ظاهر می‌شوند، معرفی کرده‌ایم. یعنی معادله پواسون اسکالر و معادله برداری با عملگر. ما نشان دادیم که با استفاده از عنصر لاگرانژ کلاسیک برای حل معادله پواسون، شرط میدان های الکتریکی مماسی پیوسته به طور طبیعی برآورده می شود. با این حال، استفاده از عنصر لاگرانژ برای حل معادله برداری به دلیل دشواری در رسیدگی به شرایط مرزی مناسب نیست.