شبیه سازی مکانیک سیالات با کامسول

شبیه سازی مکانیک سیالات با کامسول کره‌ای که کمی سبک‌تر از آب است در یک فنجان کوچک پر از مایع می‌ریزند. چگونه شکل حاصل از سطح آب و حرکت کره را هنگام شناور شدن روی سطح مدل می کنید؟ در این پست وبلاگ نحوه مدل سازی این سیستم در نرم افزار را نشان می دهیم. اگرچه ما در حال بررسی مورد یک کره کوچک هستیم، تکنیک مورد بحث در اینجا را می توان برای سایر اشکال بزرگتر نیز به کار برد.

حرکت نوسانی یک کره شناور: یک مسئله CFD
بیایید یک کره شناور را در نظر بگیریم که در یک بشر پر از آب انداخته می شود. این کره با شعاع 0.15 سانتی متر و چگالی 800 کیلوگرم بر متر مکعب، ابتدا در هوا معلق است. بشقاب استوانه ای شکل 0.65 سانتی متر و ارتفاع آن 1.7 سانتی متر است و تا حدی از آب پر شده است. اندازه سیستم به اندازه‌ای کوچک است که جریان آرام را در نظر بگیرد و همچنین اجازه می‌دهد تا فرآیند راه‌حل سریع‌تری در یک رایانه شخصی معمولی انجام شود. یک سیستم بزرگتر را می توان دقیقاً به همین روش مدل کرد، اما به منابع محاسباتی بیشتری نیاز دارد.
برای مدل‌سازی حرکت کره در سطح آب، باید جریان سیال را در هر دو فاز هوا و آب مدل‌سازی کنیم. اگر کره را صلب در نظر بگیریم، می‌توانیم حرکت آن را با حل معادلات دیفرانسیل معمولی (ODEs) حرکت محاسبه کنیم که نیرویی را که کره در حال سقوط در هوا، برخورد به سطح آب و در نهایت برهمکنش با کره تجربه می‌کند، محاسبه می‌کند. هم هوا و هم آب تنش کل سیال اعمال شده توسط سیالات بر روی مرزهای جامد داده شده است.
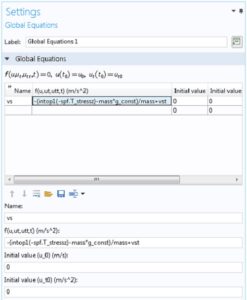
جایی که fluid نشان دهنده میدان سرعت سیال، p فشار سیال، μ ویسکوزیته دینامیکی سیال، n نرمال بیرونی به مرز، و I ماتریس هویت است. که در آن m نشان دهنده جرم، در مقابل سرعت در جهت z، و ما جابجایی در جهت z کره.

نیروی Fz را می توان با ادغام مولفه z از معادله محاسبه کرد. 1 روی سطح کره. معادلات حرکت بالا (ODEs) همراه با مدل اجزای محدود برای محاسبه جابجایی و سرعت کره حل شده است.

از آنجایی که کره از طریق هوا و آب حرکت می کند، یک مدل جریان دو فازی بر روی یک قاب فضایی با مختصات فضایی وابسته به زمان برای مدل سازی هر دو سیال فرموله شده است. قاب فضایی سیستم معمول اقلیدسی ثابت جهانی با مختصات فضایی (x,y) است. این مختصات فضایی، مربوط به گره‌های مش حوزه‌های سیال، تابع زمان هستند و مکان فعلی یک نقطه در فضا را نشان می‌دهند. این با حل مشکل جریان سیال در رابط مش متحرک به دست می آید.

انجام پروژه comsol و شبیه سازی مکانیک سیالات با کامسول

مش که مشکل جریان سیال روی آن حل شده است، با تغییر شکل مش که برابر با جابجایی کره در مرزهای رابط بین کره و حوزه سیال است تغییر شکل می‌دهد. در داخل حوزه های سیال، تغییر شکل مش با استفاده از یک روش هموارسازی مناسب که در رابط مش متحرک موجود است محاسبه می شود. تنظیم مدل.
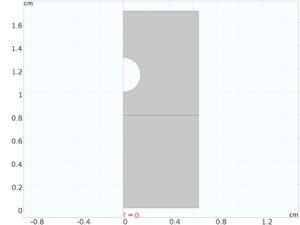
می توانیم مسئله فوق را به عنوان یک تحلیل متقارن محوری دوبعدی تنظیم کنیم. برای مدل‌سازی این مشکل، ما یک رابط جریان دو فازی را با یک رابط مش متحرک و معادلات جهانی با تعریف عبارات جفت نشان‌داده‌شده جفت می‌کنیم. هندسه مدل متقارن محوری دوبعدی که موقعیت اولیه سطح آب را با خط افقی نشان می‌دهد. کره به عنوان یک مرز در حوزه مدل نشان داده می شود زیرا ما آن را به عنوان یک شی صلب با استفاده از ODE ها مدل سازی می کنیم.

جریان سیال در این حالت آرام است، هم در فاز هوا و هم در فاز آب، بنابراین می‌توانیم از رابط لایه فاز دو فاز، فاز فیلد استفاده کنیم. (برای اطلاعات بیشتر این پست وبلاگ را در مورد نحوه انتخاب یک رابط جریان چند فازی بخوانید.) این رابط چندفیزیکی به طور خودکار یک جفت بین روش جریان آرام و میدان فاز را تعریف می کند که برای ردیابی شکل دقیق سطح آب استفاده می شود.

رابط لامینار دو فاز جریان، میدان فاز ما را قادر می سازد تا مرزهای کره را به صورت دیوارهای خیس متحرک مدل کنیم. شرایط مرزی دیوار مرطوب رابط فاز فیلد به ما امکان می دهد زاویه تماس بین سطح آب و دیوارهای جامد را مشخص کنیم، در حالی که تنظیم حرکت دیوار در شرایط مرزی دیوار رابط جریان آرام به ما امکان می دهد سرعت دیوارهای جامد متحرک را مشخص کنیم. . یک شرط مرزی خروجی برای مرز مربوط به بالای بشر استفاده می شود. انجام پروژه کامسول و شبیه سازی حرکت نوسانی یک کره شناور.

ساختار راه اندازی مدل و رابط های مختلف – یعنی جریان لایه، میدان فاز و مش متحرک – در تصویر زیر نشان داده شده است.
ما از شرایط مرزی دیوار مرطوب برای تعیین زاویه تماس بین فصل مشترک هوا و آب، دیواره های جامد بشر و کره استفاده می کنیم. برای سادگی، زاویه تماس را برای کره و دیواره های بشر یکسان فرض می کنیم.

میدان سرعت در سیالات به طور خودکار با روش میدان فاز جفت می شود تا فرارفت را محاسبه کند. خواص سیالات و ضریب کشش سطحی در کوپلینگ چندفیزیکی بین رابط‌های جریان آرام و میدان فاز مشخص شده‌اند.