شبیه سازی سنسور اثر هال
شبیه سازی سنسور اثر هال آموزش کامسول شبیه سازی نحوه مدل سازی سنسور اثر هال معمولا برای سنجش موقعیت استفاده می شود. اصل کار این است که یک میدان مغناطیسی نزدیک مسیر جریان را از طریق یک حسگر نیمه رسانا منحرف می کند. این انحراف جریان باعث تغییر پتانسیل می شود که قابل اندازه گیری است. با وجود ماهیت چندفیزیکی این دستگاه، با چند فرض، واقعاً می توان آن را به سادگی در نرم افزار مدل سازی کرد
اصول اولیه کار سنسور اثر هال
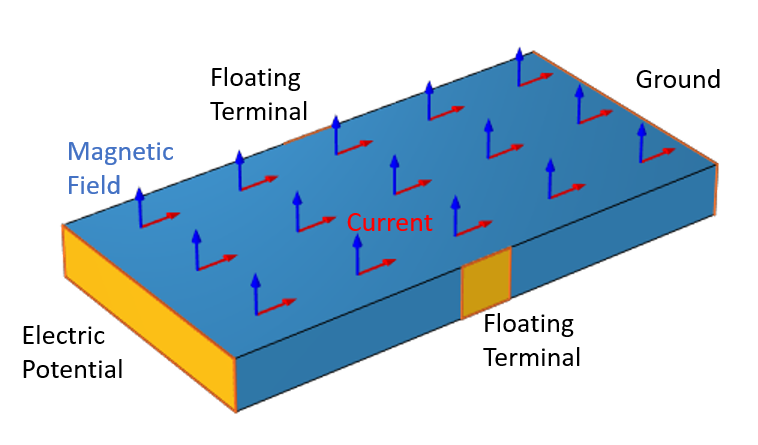
مواد نیمه رسانا با اختلاف پتانسیل الکتریکی اعمال شده در دو انتها را در نظر بگیریم که باعث جاری شدن جریان می شود. برای یک دال یکنواخت، جریان در یک خط مستقیم بین دو پایانه جریان می یابد. با این حال، به دلیل نیروی لورنتس، هر میدان مغناطیسی نزدیک این مسیر جریان را منحرف میکند، بنابراین توزیع پتانسیل الکتریکی در ماده را تغییر میدهد، و این میتواند اندازهگیری شود. برای سنسورهای معمولی اثر هال، میدان مغناطیسی به دلیل یک آهنربای نزدیک است.
یک صفحه از مواد نیمه رسانا. جریان عبوری از ماده توسط میدان مغناطیسی منحرف می شود که پتانسیل الکتریکی بین دو پایانه شناور را تغییر می دهد.
از نظر معادلاتی که در مدل محاسباتی خود استفاده خواهیم کرد، با معادله بالا شروع می کنیم و چگالی جریان را از طریق ماده نیمه رسانا به عنوان تابعی از میدان الکتریکی و میدان مغناطیسی و همچنین دو ثابت ماده اضافی می نویسیم. هدایت الکتریکی، و، ضریب هال:
![]()
یعنی اثر هال را می توان به سادگی با تعریف رسانایی الکتریکی ناهمسانگرد که تابعی از میدان مغناطیسی است، مدل سازی کرد. برای اختصار از بحث قراردادهای نشانه و اشتقاق ضریب هال در مواد مختلف صرف نظر می کنیم. این رابطه سازنده منحصر به فردی است که ما باید آن را در مدل محاسباتی خود بگنجانیم.
اکنون، در سادهترین موقعیت، میتوانیم یک میدان مغناطیسی معین را فرض کنیم و از آن برای محاسبه رسانایی الکتریکی استفاده کنیم، اما کاری که در اینجا انجام خواهیم داد، محاسبه میدان مغناطیسی متغیر و استفاده از آن برای ایجاد یک مدل چندفیزیکی واقعی است.
![]()
با این حال، قبل از شروع هر مدلسازی، چند فرض را برای ساده کردن کارها خواهیم داشت. فرض می کنیم که سرعت تغییر میدان مغناطیسی به اندازه کافی آهسته است که بتوان آن را نادیده گرفت. یعنی اگرچه معادله ماکسول-فارادی بیان می کند که:
![]()
این معادل این است که بگوییم هیچ جریان گردابی القایی قابل توجهی در دال نیمه رسانا به دلیل حرکت آهنربا وجود ندارد. یعنی میدان الکتریکی در ماده صرفاً به دلیل پتانسیل الکتریکی اعمال شده و رابطه سازنده فوق الذکر است و نه مستقیماً به دلیل تغییر زمانی میدان مغناطیسی. این فرض به ما اجازه می دهد تا مسئله را به حل میدان های مغناطیسی تقلیل دهیم.

در مرحله بعد، ما همچنین فرض میکنیم که جریانهایی که از طریق نیمهرسانا میگذرند به اندازهای کوچک هستند که خودشان در مقایسه با میدان مغناطیسی ناشی از آهنربا، هیچ میدان مغناطیسی قابلتوجهی تولید نمیکنند. این مشکل مغناطیس استاتیک را به شکل به اصطلاح بدون جریان کاهش می دهد، که در آن ما فقط باید برای یک پتانسیل اسکالر مغناطیسی حل کنیم. با این حال، توجه داشته باشید که این فرضیات برای کاری که میخواهیم انجام دهیم ضروری نیستند. ما همچنین میتوانیم میدانهای مغناطیسی ناشی از جریانها را حل کنیم، مانند یک سیمپیچ مجاور. این فقط مدل ما را از نظر محاسباتی کمی گران تر می کند.
در نهایت، ما همچنین فرض می کنیم که رسانایی ماده به اندازه کافی بزرگ است به طوری که ثابت زمانی RC بسیار کوتاهتر از هر تغییر زمانی است که ما به آن علاقه داریم. یعنی ما می توانیم در هر لحظه از زمان، جریان های الکتریکی را درمان کنیم. مدل به عنوان یک وضعیت کاملا ایستا، از آنجایی که ما فرض کردهایم که تمام عبارات مشتق زمانی بیاهمیت هستند. بنابراین، مسئله الکتریکی به حل معادله پتانسیل الکتریکی ساکن کاهش مییابد، البته با رسانایی الکتریکی ناهمسانگردی که از نظر مکانی متغیر است که تابعی از میدان مغناطیسی است.
![]()
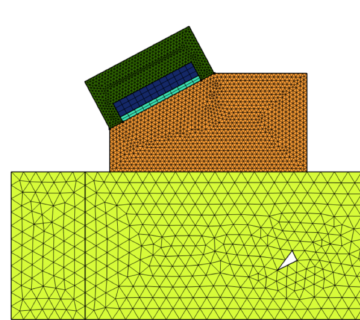
در تصویر زیر وضعیت را در نظر خواهیم گرفت. یک آهنربای استوانه ای کوچک روی یک چرخ آهنی در حال چرخش نصب شده است. در زیر، یک دامنه مستطیلی وجود دارد که نشان دهنده سنسور است.
ابتدا میدان های مغناطیسی را با استفاده از رابط میدان های مغناطیسی، بدون جریان حل می کنیم. علاوه بر دامنههای تصویر بالا، فضای هوایی اطراف آنها و همچنین یک دامنه برش عنصر نامحدود را مدلسازی میکنیم.
برای حل این مشکل، میدان های مغناطیسی را محاسبه می کنیم و سپس می توانیم به مدل سنسور اثر هال برویم. در حوزه نیمه هادی از رابط جریان های الکتریکی استفاده می کنیم. شرایط زمین و ترمینال در انتهای مخالف ماده اعمال می شود و دو شرط پتانسیل شناور در هر طرف اعمال می شود.
رسانایی الکتریکی را می توان تابعی از میدان مغناطیسی متغییر مکانی ساخت، که ما فقط آن را محاسبه کردیم، اما مایلیم چرخش چرخ را نیز در نظر بگیریم. سادهترین راه برای در نظر گرفتن چرخش، انجام یک Sweep پارامتریک است، اما این در واقع کمی بیشتر از چیزی است که در اینجا باید انجام دهیم. میدانهای مغناطیسی از طریق سنسور در حال چرخش هستند، اما ما فرض کردیم که تحت تأثیر خود سنسور قرار نمیگیرند.

در این شرایط، ما فقط میتوانیم از یک نقشهبرداری چرخشی برای تغییر میدان مغناطیسی به عنوان تابعی از یک پارامتر سراسری، Angle، از طریق عملگر General Extrusion، مشابه آنچه در این پست وبلاگ قبلی توضیح داده شد، استفاده کنیم. با این حال، در این مورد، ما یک میدان برداری را میچرخانیم، بنابراین خود بردارها را نیز از طریق یک ماتریس چرخش سهبعدی میچرخانیم. دو اسکرین شات زیر پیاده سازی را نشان می دهد و مجموعه ای از متغیرهای میدان مغناطیسی چرخشی را تعریف می کند.