شبیه سازی تشعشع نیمرسانا با کامسول
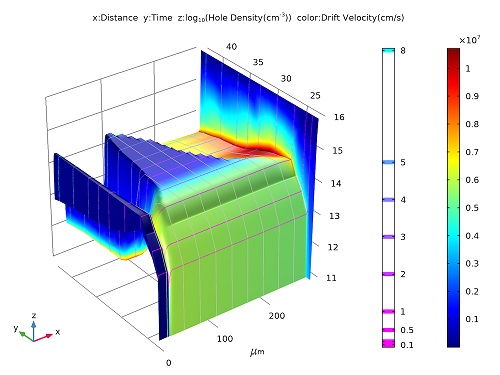
شبیه سازی تشعشع نیمرسانا با کامسول اثرات تشعشع در نیمه هادی ها موضوعی گسترده و پیچیده است که بر بسیاری از حوزه های فنی مانند صنعت الکترونیک، تصویربرداری پزشکی، مهندسی هسته ای و کاربردهای هوافضا و نظامی تأثیر می گذارد. در اینجا، ما به شما نشان می دهیم که چگونه پاسخ الکترونیکی یک دیود p-i-n (با نام مستعار دیود PIN) به تشعشعات یونیزان را بر اساس یک مقاله اولیه مطالعه کنید. این آموزش با ماژول نیمه هادی در دسترس است. تعریف پارامتر زمان جهانی برای مطالعه هر دو پاسخ حالت پایدار و گذرا، به تعریف یک پارامتر سراسری t با واحد زمان، و یک نرخ تولید وابسته به زمان gR با استفاده از پارامتر سراسری t و یک تابع تکهای سراسری pw1 کمک میکند، که در این مدل، یک پالس مثلثی با حداکثر مقدار واحد توصیف میکند. این پارامتر زمانی t به حلکنندههای ثابت اجازه میدهد تا متغیر زمان داخلی با همان نام t را تشخیص دهند. این امر امکان تنظیم آسان مدل را با استفاده از همان بیان وابسته به زمان gR برای نرخ تولید ناشی از دوز تابش، بدون توجه به نوع مطالعه ممکن میسازد. برای جمعآوری حاملهای بار تولید شده توسط تابش، بایاس معکوس به ۱ کیلو ولت میشود. . این کار با مطالعات ثابت در مدل انجام می شود. مقدار پارامتر زمان t در مقدار 0[s] همانطور که در جدول پارامترهای جهانی مشخص شده است باقی می ماند، به طوری که تابش صفر (بدون تولید) برای جابجایی ولتاژ باشد.
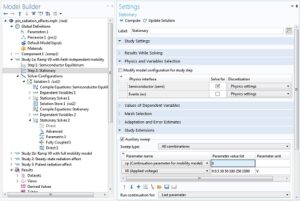
آموزش کامسول پاسخ حالت پایدار
مدل تحرک وابسته به میدان که توسط مقاله استفاده میشود، سیستم معادله را بسیار غیرخطی و حل آن را دشوار میسازد. خوشبختانه راه های مختلفی برای غلبه بر این مشکل وجود دارد. برای مثال، ابتدا میتوانیم تحرک مستقل از میدان را با صفر کردن پارامتر continuation cp فرض کنیم. این کمک می کند تا ولتاژ اعمال شده V0 از حالت تعادل به ولتاژ عملیاتی 1000 ولت افزایش یابد. در این مرحله، همچنین به تغییر پیش بینی ادامه از ثابت پیش فرض به خطی کمک می کند. گزینه Linear با استفاده از یک طرح برون یابی خطی برای تخمین حدس اولیه برای پارامتر جاروب بعدی به سرعت بخشیدن به جابجایی ولتاژ کمک می کند. گزینه ثابت پیش فرض از راه حل فعلی به عنوان حدس اولیه برای پارامتر جاروب بعدی استفاده می کند، که رویکرد محافظه کارانه تری است و در بیشتر موارد برای سیستم معادلات نیمه هادی بسیار غیر خطی مناسب است – اما برای این مدل، خیلی محافظه کارانه است. جارو ولتاژ با تحرک مستقل از میدان کامل می شود، ما می توانیم از مجموعه راه حل ها به عنوان حدس اولیه برای مورد مدل تحرک کامل با وابستگی به میدان استفاده کنیم. این کار با استفاده از یک گره Sweep Parametric برای جفت کردن ولتاژ جابجایی V0 با شاخص پارامتر جابجایی انجام می شود.
آموزش کامسول شبیه سازی تشعشع نیمرسانا با کامسول
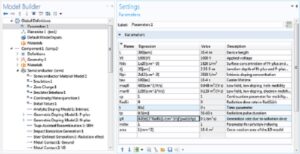
با بایاس کاملا معکوس دیود در 1000 ولت، ما آماده مطالعه پاسخ دستگاه به تشعشعات حالت پایدار هستیم. همانطور که قبلاً ذکر شد، در مطالعات قبلی پارامتر زمان t طبق جدول پارامترهای جهانی 0[s] بود، بنابراین تابع پالس pw1(t/tp) صفر و نرخ تولید ناشی از تابش gR نیز صفر بود. حال، برای تعیین تابش غیر صفر، فقط پارامتر زمان t را روی مدت زمان پالس tp تنظیم کنید، به طوری که تابع پالس pw1(t/tp) واحد باشد. سپس، نرخ دوز را می توان با پارامتر Rad به طور مستقیم در واحدهای Rad(Si)/s تعیین کرد. با این حال، سیستم معادلات را نیز بسیار غیرخطی و حل آن را دشوار می کند. در جفت مطالعات قبلی برای جارو کردن ولتاژ، این مشکل با تفکیک فرآیند حل به دو مرحله، با تحرک مستقل از میدان در مرحله اول و تحرک کامل در مرحله دوم، برطرف شد. در این مطالعه فعلی از جارو نرخ دوز، ما یک روش جایگزین برای غلبه بر دشواری با استفاده از یک مطالعه واحد با تحرک کامل نشان میدهیم.
اگر علاقه مند به مباحث آموزش comsol شبیه سازی انتقال حرارت بافت کامسول هستید مطالعه کنید.
غیرخطی بودن باعث می شود که حلگر نیوتن خودکار کندتر از رفتار همگرایی درجه دوم ایده آل همگرا شود، که به نوبه خود باعث می شود که حلگر ادامه دهنده گام های بسیار کوچکی برای پارامتر جاروب شده Rad بردارد. در عوض، می توانیم از گزینه نیوتن ثابت با ضریب میرایی مناسب استفاده کنیم. علاوه بر این، ما اندازه گام اولیه بهتری را برای حلکننده ادامه در زیر گره Parametric ارائه میکنیم تا از برداشتن گام اول بیش از حد بزرگ و سپس اتلاف زمان در عقبنشینی جلوگیری کنیم. در نهایت، میتوانید از شتاب اندرسون برای بهبود بیشتر عملکرد استفاده کنید (با بهرهگیری از اطلاعات تاریخچه قبلی تکرار غیرخطی)، و از حداکثر تعداد تکرارهای کوچکتر برای کاهش زمان تلفشده در عقبگردی استفاده کنید. پاسخ وابسته به زمان.
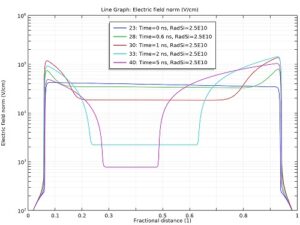
پس از تکمیل مطالعه حالت پایدار، اکنون آماده بررسی اثر تشعشعات پالسی با شکل موج مثلثی ارائه شده توسط شکل 8 در مقاله مرجع هستیم. این شکل موج توسط تابع پالس pw1(t/tp) در مدل با ارتفاع یکسانی نرمال شده ارائه می شود. نرخ پیک دوز با پارامتر Rad در واحد Rad(Si)/s مشخص می شود. ما تحمل حلگر وابسته به زمان را به 1e-8 می کنیم و از مقیاس بندی مبتنی بر مقدار اولیه برای متغیرهای وابسته استفاده می کنیم، زیرا شرایط اولیه توسط حل مطالعه ثابت و اثر گذرا یک اغتشاش کوچک از نظر مقیاس کلی متغیرهای وابسته است. همچنین، میتوانیم از یک رابط رویدادها برای ثبت تغییر ناگهانی شیب در انتهای پالس تابش اعمال شده استفاده کنیم.