شبیه سازی ترمودینامیک و هیدروداینامیک کامسول
شبیه سازی ترمودینامیک و هیدروداینامیک کامسول صنعت الکترونیک به طور فزایندهای دستگاههای الکترونیکی کوچکتری را تولید میکند که گرمای تولید میکنند که باید دفع شود. شواهد مشاهده شده نشان می دهد که در مقیاس های کوتاه تر، استخراج گرما دشوارتر از آنچه قانون فوریه پیش بینی می کند، نشان می دهد که اعتبار محدود آن است. تمرکز تحقیق فعلی ما حل این مشکل باز است.
استفاده از قانون فوریه برای توصیف انتقال حرارت
در سال 1822، فوریه Théorie Analytique de la Chaleur (نظریه تحلیلی گرما) را منتشر کرد. از آن زمان، قانون فوریه با موفقیت برای توصیف بسیاری از مشاهدات تجربی مختلف در سیستمهای مختلف – با نتایج قابلتوجهی استفاده شده است. قانون فوریه با یک رابطه ساده بین گرادیان حرارتی و شار گرما توصیف می شود.
در چند دهه گذشته، شواهد نشان داده است که معادله (1) در تجزیه و تحلیل دستگاه هایی با طول مشخصه L کوچکتر از میانگین مسیر آزاد حامل های گرما (فونون) صحیح نیست. جریان گرمای مشاهده شده بسیار کوچکتر از آنچه توسط قانون فوریه پیش بینی شده است می شود و ظرفیت این اجزا برای آزادسازی گرمای اضافی را بدتر می کند. این مسئله معمولاً با استفاده از یک هدایت حرارتی مؤثر بسته به طول مشخصه حل می شود که باید به طور تجربی تعیین شود.
نظریه جنبشی به ما امکان می دهد پیش بینی صحیح هدایت حرارتی را در هندسه های ساده بدست آوریم، اما کاربرد آن در حال حاضر در هندسه پیچیده یک دستگاه الکترونیکی امکان پذیر نیست.
آموزش کامسول ترمودینامیک
معرفی مدل جنبشی- جمعی برای حمل و نقل حرارتی هیدرودینامیکی
مدل جنبشی-جمعی (KCM)، که در UAB توسعه یافته است، یک چارچوب نظری است که بر توصیف انتقال گرما در مقیاس نانو و میکرو، و همچنین محاسبه پارامترهای انتقال مربوطه که در معادلات از محاسبات میکروسکوپی ظاهر میشوند، متمرکز است. تنها با این ترکیب محاسبات است که می توانیم یک مدل پیش بینی به دست آوریم.
تصحیح مرتبه اول قانون فوریه معادله Guyer-Krumhansl است.
توجه کنید که عبارت جدید لاپلاسی در معادله (2) قانون فوریه را به قانونی شبیه معادله استوکس برای یک سیال چسبناک تغییر می دهد. به همین دلیل، رفتار زیر معادله (2) معمولاً هیدرودینامیک فونون نامیده می شود. اصطلاح جدید ویسکوزیته گرمایی را معرفی می کند که رسانایی موثر را در مناطقی که شار همگن نیست کاهش می دهد. در این مناطق، شار گرما و گرادیان دما دیگر موازی نخواهند بود که پیامدهای مهمی برای توزیع گرما و دما دارد.
آموزش comsol هیدروداینامیک
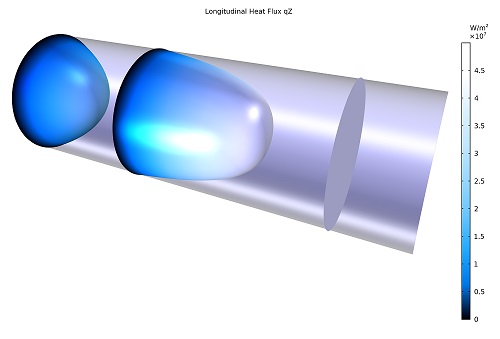
تجزیه و تحلیل پیامدهای مختلف معادله مفید است. (1) و معادلات (2-3) با استفاده از یک هندسه ساده مانند یک نانوسیم. در تصویر زیر جریان گرما را در داخل یک نانوسیم با شعاع 500 نانومتر مشاهده می کنیم که از یک طرف آن گرم شده و از طرف دیگر خنک می شود. دماهای سرد و گرم در انتهای مخالف سیم اعمال می شود و شرایط دوره ای برای شار استفاده می شود تا از اثرات مرزی روی پروفیل جلوگیری شود. مشخصات دما در همه موارد یکسان است: یک گرادیان ثابت در جهت طولی بدون تغییر در جهت عرضی. شار برای محدودهای از موقعیتها با مقدار ویسکوزیته رو به افزایش، از قانون فوریه () تا مقدار نانومتر رسم میشود. تفاوت اصلی را می توان به راحتی مشاهده کرد: در حالی که معادله. (1) یک شار ثابت بر روی مقطع می دهد، معادله. (2-3) یک پروفیل جریان منحنی ارائه می دهد. انحنای شار حرارتی ظاهر می شود زیرا اثر مرز جریان را در ناحیه ای از عرض کاهش می دهد. هنگامی که در مقایسه با شعاع سیم () کوچک باشد، نشان داده میشود که جریان فقط در یک پوسته استوانهای نزدیک به مرز تحت تأثیر قرار میگیرد که لایه نادسن نامیده میشود. در خارج از این لایه، مقدار جریان حرارتی مربوط به حد فوریه بازیابی می شود. اگر علاقه مند به مباحث شبیه سازی مواد و پلیمر کامسول هستید از اینجا بخوانید.
شبیه سازی ترمودینامیک و هیدروداینامیک کامسول در مرکز کامسول پروژه انجام میپذیرد.
هنگامی که طول مشخصه به همان ترتیب شعاع سیم باشد، لایه نادسن افزایش مییابد تا زمانی که اثرات در مرکز نیز مشاهده شود. در این نقطه، جریان در همه جای مقطع نمونه کاهش مییابد و پروفیل جریان شباهتهایی با جریان Poiseuille سهموی برای سیالات ویسکوز نشان میدهد.
همانطور که قبلاً اشاره کردیم، مهمترین جنبه تعیین معادله انتقال حرارتی در نانوسیم ها این است که نمی توان به طور تجربی مشخصات شار حرارتی را در سطح مقطع بدست آورد. تنها قدری که میتوان اندازهگیری کرد رسانایی گرمایی مؤثر است که به عنوان شار متوسط بر سطح مقطع تقسیم بر گرادیان دما تعریف میشود. این ما را از تمایز تجربی تشخیص نمیدهد که آیا رفتاری را مشاهده میکنیم که از معادله Guyer-Krumhansl پیشبینی میشود یا صرفاً یک رفتار از معادله. (1) با کاهش هدایت حرارتی موثر.