روش Beam Envelopes برای شبیه سازی اپتیک موج کامسول

روش Beam Envelopes برای شبیه سازی اپتیک موج کامسول در حوزه نوری موج، شبیه سازی سیستم های نوری بزرگ به روشی که معادله ماکسول را به طور دقیق حل کند، دشوار است. این به این دلیل است که امواجی که در سیستم ظاهر می شوند باید توسط یک شبکه به اندازه کافی ریز حل شوند. روش beam envelopes در نرم افزار یکی از گزینه ها برای این منظور است. در این پست وبلاگ، نحوه استفاده از رابط امواج الکترومغناطیسی، Beam Envelopes و مدیریت محدودیت های آن را مورد بحث قرار می دهیم.
مقایسه روش‌های حل مدل‌های اپتیک موج بزرگ
در شبیه‌سازی‌های الکترومغناطیسی، برای یافتن جواب دقیق معادلات ماکسول، طول موج همیشه باید توسط مش حل شود. این نیاز، شبیه سازی مدل هایی را که در مقایسه با طول موج بزرگ هستند، دشوار می کند. روش های مختلفی برای مشکلات اپتیک موج ثابت وجود دارد که می تواند مدل های بزرگ را مدیریت کند. این روش ها شامل فرمول های به اصطلاح پراش، مانند فرمول پراش فراونهوفر، فرنل-کیرشهوف، و رایلی-سومرفلد و روش انتشار پرتو (BPM)، مانند BPM پاراکسیال و روش طیف زاویه ای (مرجع 1) می شود.
اکثر این روش ها از تقریب های خاصی برای معادله هلمهولتز استفاده می کنند. این روش‌ها می‌توانند مدل‌های بزرگ را مدیریت کنند، زیرا مبتنی بر روش انتشار هستند که میدان را در یک صفحه از یک میدان شناخته شده در صفحه دیگر حل می‌کند. بنابراین لازم نیست کل دامنه را مش کنید، فقط به یک مش دوبعدی برای صفحه مورد نظر نیاز دارید.
در مقایسه با این روش‌ها، رابط امواج الکترومغناطیسی، پوشش‌های پرتو (که در ادامه پست وبلاگ از آن به عنوان رابط پاکت پرتو یاد می‌کنیم) حل دقیق معادله هلمهولتز را در یک دامنه حل می‌کند. این می تواند مدل های بزرگ را اداره کند. به عنوان مثال، اگر محدودیت خاصی برآورده شود، نیاز مش بندی می تواند به طور قابل توجهی کاهش یابد.

تئوری پشت رابط پاکت پرتو و آموزش کامسول 

بیایید نگاهی به ریاضیاتی بیندازیم که رابط Beam Envelopes «زیر کاپوت» محاسبه می‌کند. اگر این رابط را به یک مدل اضافه کنید و روی گره Physics Interface کلیک کنید و Type of Phase specification را به User defined تغییر دهید، در قسمت Equation موارد زیر را مشاهده خواهید کرد.
معادله اول، معادله حاکم برای رابط Beam Envelopes، می تواند با جایگزین کردن تعریف دوم میدان الکتریکی به معادله هلمهولتز استخراج شود. اگر بدانیم، تنها مجهول است و می توانیم آن را حل کنیم. برای حل مشکل باید فاز، , پیشینی داده شود.
با معادله دوم، شکلی را در نظر می گیریم که قسمت نوسان سریع، فاز، از میدان خارج شود. اگر این درست باشد، پاکت به آرامی در حال تغییر است، بنابراین ما نیازی به تعیین طول موج نداریم. در عوض، ما فقط باید موج آهسته پاکت را حل کنیم. به دلیل این فرآیند، شبیه سازی مشکلات اپتیک امواج در مقیاس بزرگ در رایانه های شخصی امکان پذیر است.
یک سوال رایج این است: “چه زمانی پاکت را به جای خود میدان می خواهید؟” شبیه سازی لنز یک مثال است. گاهی اوقات ممکن است به شدت به جای میدان الکتریکی پیچیده نیاز داشته باشید. در واقع، مربع هنجار پاکت، شدت را می دهد. در چنین مواردی، برای دریافت تابع پاکت کافی است. جهت آموزش comsol اقدام کنید.
اگر عملکرد فاز به طور دقیق شناخته نشود چه اتفاقی می افتد؟

مدل سازی با روش Beam Envelopes برای شبیه سازی اپتیک موج کامسول

ریاضی پشت روش پاکت پرتو سوالات بیشتری را معرفی می کند:
اگر فاز به طور دقیق مشخص نباشد چه؟
آیا می توانیم در چنین مواردی از رابط Beam Envelopes استفاده کنیم؟
آیا نتایج صحیح است؟
برای پاسخ به این سوالات، باید کمی بیشتر ریاضیات را انجام دهیم.
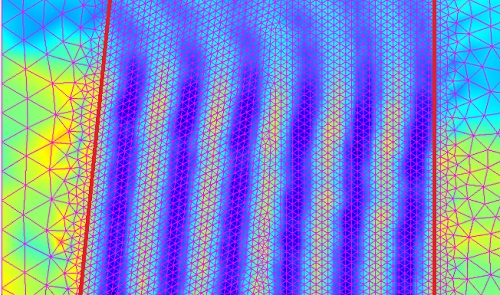
بیایید ساده ترین حالت آزمایشی را در نظر بگیریم: یک موج مسطح، که در آن برای طول موج = 1 um، در یک حوزه مستطیلی به طول 20 um منتشر می شود. (ما عمداً از یک دامنه کوتاه برای اهداف توضیحی استفاده می کنیم.)

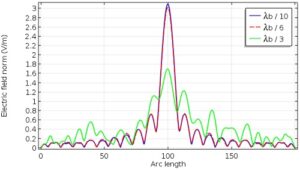
موج خارج از صفحه از مرز چپ وارد می شود و مرز سمت راست را بدون بازتاب ارسال می کند. این را می توان در رابط Beam Envelopes با افزودن یک شرط مرزی Matched با تحریک در سمت چپ و بدون تحریک در سمت راست، در حالی که یک شرط مرزی رسانای مغناطیسی کامل در بالا و پایین اضافه کرد (به این معنی که ما به y اهمیت نمی دهیم) شبیه سازی شود. جهت).
تنظیم صحیح برای مشخصات فاز در شکل زیر نشان داده شده است. این یک ترفند نیست. درعوض، می بینیم که اگر تابع فاز خاموش باشد، تابع پاکت نیز خاموش می شود، زیرا به صورت ضربانی پیچیده می شود. با این حال، هنجار میدان الکتریکی هنوز هم می تواند درست باشد. بنابراین، برای بدست آوردن میدان الکتریکی صحیح، مهم است که تابع پاکت پیچ خورده به درستی محاسبه شود. نمودارهای بالا به وضوح این را نشان می دهد. محفظه مش شش عنصری هنجار میدان الکتریکی کاملاً صحیح را ارائه می دهد زیرا عملکرد پاکت پیچ خورده را به طور کامل حل می کند. مش های دیگر بسته به اندازه مش یک راه حل تقریبی برای عملکرد پاکت پیچ خورده ارائه می دهند. آنها همچنین این کار را برای هنجار میدانی انجام می دهند. این یک نتیجه کلی است که برای موارد دلخواه صادق است.