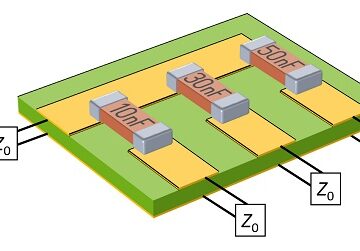
تجزیه و تحلیل منحنی های پراکندگی با کامسول

تجزیه و تحلیل منحنی های پراکندگی با کامسول فرض کنید یک سیستم بسیار طولانی با سطح مقطع ثابت دارید: یک لوله پر از مایع. مدلسازی این سیستم از نظر محاسباتی پرهزینه و زمان بر است. با استفاده از رویکرد انتشار موج هدایت‌شده، می‌توانید مقطعی از سیستم را مدل‌سازی کنید و امواج هدایت‌شده را در امتداد آن محاسبه کنید. شما می توانید چنین امواجی را با استفاده از منحنی های پراکندگی نمایش دهید. در اینجا، ما یک تجزیه و تحلیل همراه با در نظر گرفتن هوا و آب را مورد بحث قرار می دهیم
به عنوان مایعات داخلی ما همچنین پویایی سیستم را با استفاده از منحنی های پراکندگی تجزیه و تحلیل می کنیم.

آموزش کامسول لوله های پر از مایع

لوله های پر از مایع که به آنها سازه های حامل مایع نیز گفته می شود، کاربردهای صنعتی زیادی مانند خطوط لوله گاز، صدا خفه کن خودرو، بدنه هواپیما و خطوط لوله زیر آب دارند. اندازه یک سیستم خط لوله می تواند از سانتی متر تا کیلومتر متغیر باشد.

مدل‌سازی سیستم‌های لوله‌های بزرگ با نرم‌افزارهای شبیه‌سازی دشوار است و به دلیل حالت های آکوستیک و الاستیک به طور مستقل وجود ندارند، تجزیه و تحلیل فردی آن را آسان نمی کند. بنابراین، باید بر تأثیر بارگذاری سیال بر پاسخ لوله تأکید کنیم.

در فرکانس های پایین، مدت بارگذاری سیال به کوچکی تمایل دارد، بنابراین پاسخ سیستم تحت تسلط دینامیک سازه/لوله است (مرجع 2). بارگذاری سیال ویژگی های ارتعاشی سازه در تماس و در نتیجه تابش صوتی را تغییر می دهد. اثرات بارگذاری سیال قوی ترین توسط

ساختارهای در تماس با سیالات متراکم تر، زیرا نیروهای سیال با چگالی متوسط سیال متناسب است.

منحنی های پراکندگی چیست؟

به طور کلی، سیستم ها را می توان با جرم توزیع شده و سختی توصیف کرد. درجات آزادی بی نهایت (DOF) برای یک سیستم پیوسته وجود دارد که منجر به حالت های بی نهایت می شود. برای یک محدوده فرکانس محدود، تعداد محدودی از حالت‌ها وجود دارد که می‌توان آن‌ها را به صورت جداگانه با استفاده از تجزیه مودال تحلیل کرد. حرکت چنین سیستم های پیوسته با معادلات دیفرانسیل جزئی (PDEs) از روابط نیرو/شتاب و نیرو/تغییر شکل توصیف می شود. نمونه هایی از این سیستم ها عبارتند از رشته ها، میله ها و شفت ها (PDE های مرتبه دوم) و همچنین تیرها (PDE های مرتبه چهارم) و لوله های پر از مایع.

حل چنین معادلاتی را می توان با استفاده از دو رویکرد تجسم کرد:

آموزش کامسول حالت های ویژه

آموزش comsol نمایش موج (یا حالت های موج)

فرض کنید ما علاقه مند به مدل سازی دینامیک یک سیستم بزرگ در فرکانس های بالاتر با استفاده از روش اجزاء محدود (FEM) هستیم. برای ثبت رفتار آن، طول موج باید با تعداد کافی عنصر گسسته شود، که می تواند منجر به تعداد زیادی DOF و حافظه و زمان بیشتر شود. ما می‌توانیم با استفاده از حالت‌های موج یا نمایش سیستم به‌عنوان امواج هدایت‌شونده با این مشکل مقابله کنیم، زیرا امواج قبل از فروپاشی، مسافت‌های زیادی را طی می‌کنند.

خواص موج یکی دیگر از مزایای رویکرد مبتنی بر موج است. آنها برای مطالعه ساختاری مهم هستند

صدا، پاسخ فرکانسی موجبرهای با طول محدود و محاسبه انتقال انرژی از طریق ساختارها. شما این حالت‌های موج را از طریق منحنی‌های پراکندگی نشان می‌دهید، که رابطه‌ای بین تعداد موج و فرکانس ایجاد می‌کند.

منحنی های پراکندگی اساساً خطوط جداگانه ای هستند که هر کدام یک حالت جداگانه را نشان می دهند. تنها پیش نیاز روش مبتنی بر موج ثابت بودن سطح مقطع سیستم است (محدودیتی برای طول وجود ندارد). برای مدل‌سازی سیستم‌های طولانی، مانند لوله‌های حامل سیال، تیرها یا مسیر ریلی، رویکرد مبتنی بر موج بسیار مفید است.

استفاده از منحنی های پراکندگی برای تجزیه و تحلیل لوله های پر از مایع

امواج در زمان و مکان منتشر می شوند. تغییرات فضایی با کمیتی توصیف می‌شود که نشان‌دهنده تغییر فاز در واحد فاصله است و برابر با ω/c است. این عدد موج است که با k نشان داده می شود. یک طول موج مربوط به اختلاف فاز وابسته به x 2π است: kλ = 2π.

هنگامی که یک سیستم با نیرویی در یک انتها برانگیخته می شود، تعداد زیادی امواج شروع به انتشار به سمت دیگر می کنند. هر موج با سرعتی حرکت می کند که به عنوان سرعت فاز (مستقل از ω؛ به عنوان مثال، امواج برشی طولی) و سرعت گروهی (وابسته به فرکانس؛ به عنوان مثال، امواج خمشی) توصیف می شود. همه امواج با هم زیر یک پاکت حرکت می کنند. سرعت انتقال انرژی با سرعت گروهی داده می شود، که سرعت پوشش داده شده توسط cg = ∂ω/∂k است.

تجزیه و تحلیل یک قیف یون الکترودینامیکی

منحنی های پراکندگی دینامیک یک سیستم جفت شده را توضیح می دهند. در لوله‌های پر از مایع که امواج می‌توانند در سیال و همچنین در دیواره لوله حرکت کنند، منحنی‌های پراکندگی یک عدد موج مشترک یا حالت موجی را ارائه می‌کنند که در کل سیستم منتشر می‌شود. منحنی های پراکندگی همچنین بینشی را در مورد آنچه در داخل سیستم در فرکانس های مختلف اتفاق می افتد ارائه می دهد.