آموزش کامسول در مورد تلفات انتقال برق سه فاز

آموزش کامسول در مورد تلفات انتقال برق سه فاز دارای محاسبات پیچیده ای است. به نظر می رسد که آرایش هندسی خاصی از هادی ها در یک خط انتقال منجر به عدم تعادل تلفات بین سیم ها می شود، حتی اگر ساختار به نظر متقارن باشد. ما یک مدل ساده برای نشان دادن این موضوع ساختیم، که در این مقاله به شرح توضیح داده خواهد شد.

آموزش کامسول محاسبات تلفات در سیم ها

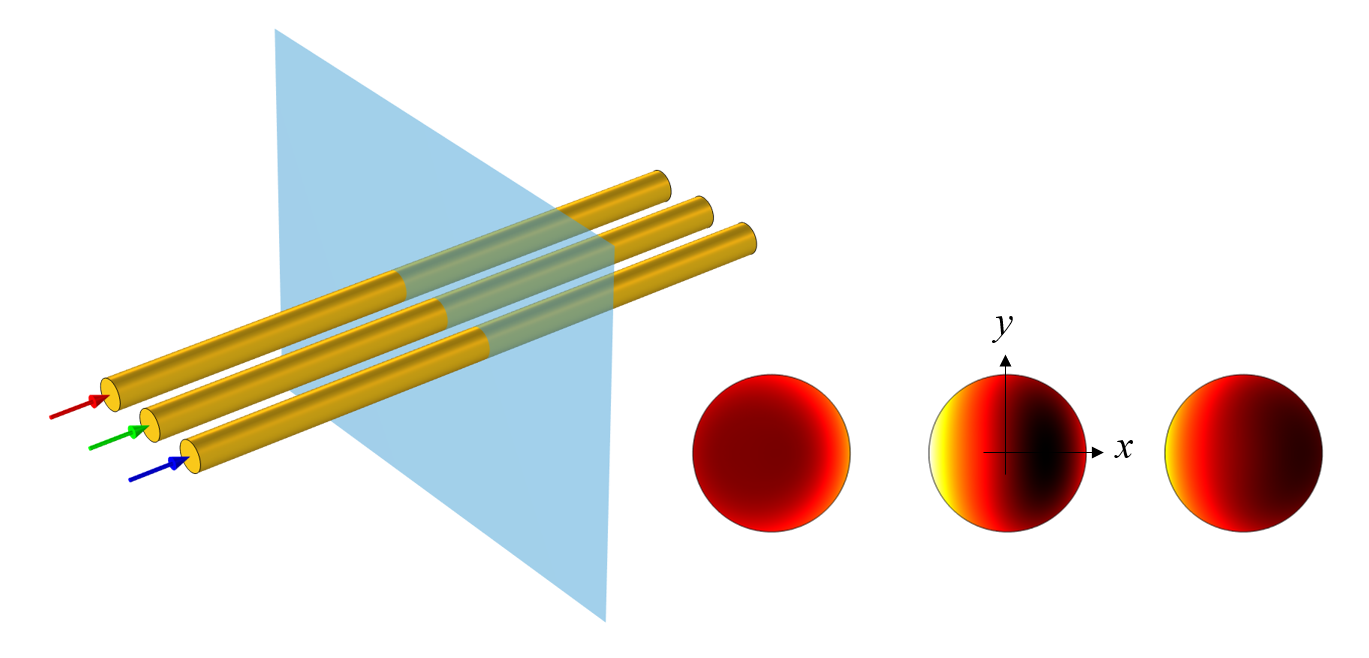
فرض کنید سه سیم مسی یکسان داریم که در یک خط افقی به یک اندازه فاصله دارند و برق سه فاز را حمل می کنند. تلفات در هر سیم چقدر خواهد بود؟ این وضعیت در شماتیک زیر در سمت چپ نشان داده شده است. ما فرض کردیم که سیم ها بسیار بلند و دارای سطح مقطع ثابت هستند، بنابراین مدل را به یک مدل مقطعی دو بعدی کاهش دادیم که در حوزه فرکانس حل شده است. ما هر سیم را در نرم افزار  کامسول پروژه با استفاده از شرایط دامنه سیم پیچ و همچنین اعداد مختلط برای تعریف جریان های اعمال شده که 120 درجه خارج از فاز با یکدیگر هستند، مدل کردیم. برای یک آموزش عمیق در مورد مدل سازی خطوط انتقال سه فاز، سری آموزش کابل ما را ببینید. شایان ذکر است که جریان‌هایی که از هر سه سیم عبور می‌کنند به صفر می‌رسند، بنابراین نیازی نیست خودمان را در مورد مسیر برگشت جریان در امتداد یک مرز نگران کنیم. توزیع تلفات در هر سیم در شکل زیر در سمت راست نشان داده شده است.

شروع با یک مورد متفاوت که می تواند تقریب خوبی باشد

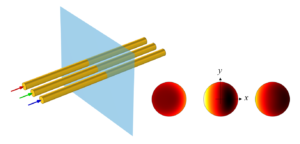
راه های مختلفی برای مدلسازی از طریق این نرم افزار وجود دارد. در اینجا، ما با اعمال یک تغییر هندسی شروع می کنیم که درک همه چیز را ساده تر می کند، و سپس خواهیم دید که این درک ما را به کجا می برد. بیایید هادی ها را به صورت مثلثی متساوی الاضلاع، همانطور که در تصویر زیر در سمت چپ نشان داده شده است، مرتب کنیم. حل این مورد نشان می دهد که همه هادی ها تلفات کل یکسان و توزیع تلفات یکسان دارند. همچنین شایان ذکر است که توزیع تلفات به صورت چرخشی متقارن است. یعنی چرخش 120 درجه در اطراف مرکز، توزیع یکسانی را ایجاد می کند. حالا بیایید روی درک اینکه چرا میدان ها متقارن هستند کار کنیم و ببینیم که چگونه به ما در درک حالت اصلی کمک می کند.

هنگامی که جریان AC از طریق یک سیم منفرد هدایت می شود، میدان مغناطیسی متغیر با زمان، جریان هایی را در خود سیم القا می کند. این جریان های ناشی از برگشت تمایل به مخالفت با جریان محرکه دارند، به ویژه در مرکز سیم، که منجر به به اصطلاح اثر پوستی می شود. علاوه بر جریان القایی برگشتی روی خود سیم، اثر مجاورت منجر به القای جریان محرک در دو هادی مجاور می شود. ما، هر چند بدون اثبات رسمی، بیان خواهیم کرد که این جریان های القایی در سیم های همسایه عبارتند از:

از نظر قدر یکسان است، زیرا دو هادی مجاور هم اندازه و فاصله دارند

120 درجه خارج از فاز با یکدیگر

هنگامی که جریان سه فاز از هر سه سیم عبور می کند، کل جریان یکی از این سه سیم مجموع جریان محرک در آن سیم است. جریان برگشتی و جریان های القایی از سیم های مجاور، به عنوان مثال، . ولتاژ اعمالی مورد نیاز برای راه اندازی جریان سه فاز متناسب با جریان محرکه است و به صورت زیر داده می شود: مقاومت سیم DC کجاست. هنگام استفاده از ویژگی کویل برای راه اندازی این سیم ها، یک معادله جهانی اضافی به سیستم معادلات اضافه می شود. این ولتاژ را حل می کند که جریان کل مورد نظر را القا می کند. مجموع تلفات در هر سیم به صورت زیر نشان داده می شود که در آن جریان ها و ولتاژها دارای مقادیر پیچیده و 120 درجه خارج از فاز با یکدیگر هستند. مقاله مرتبط با شبیه سازی پیزوالکتریک اینجا بخوانید.

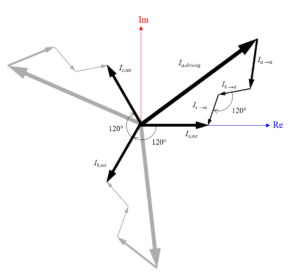
حال بیایید این جریان‌ها را در صفحه مختلط رسم کنیم، که به ما کمک می‌کند تجسم کنیم که چگونه این سه جریان القایی برگشتی با جریان کل جمع می‌شوند. ما در واقع اندازه یا فاز واقعی هیچ یک از این اصطلاحات را نمی دانیم، اما می دانیم که فاز جریان های القایی از دو سیم همسایه 120 درجه خارج از فاز با یکدیگر هستند. همچنین می توانیم به طور منطقی فرض کنیم که بزرگی نسبی جریان ها عبارتند از: . این اطلاعات و فرض به ما اجازه داد تا طرح زیر را بسازیم. میتوان برای آموزش comsol اقدام کنید.

Losses in Three-Phase Transmission Lines

بیایید ولتاژهای محرک با ارزش پیچیده را که روی همه سیم‌ها ثابت شده‌اند در نظر بگیریم و به این فکر کنیم که وقتی سیم‌ها را از آرایش متساوی الاضلاع به آرایش خطی منتقل می‌کنیم چه اتفاقی می‌افتد. سیم مرکزی را به صورت برچسب گذاری می کنیم. جریان های القای برگشتی، به عنوان مثال، تغییر نخواهند کرد و جریان های القایی از سیم مرکزی به سیم های جانبی همچنان از نظر بزرگی برابر خواهند بود: . آموزش کامسول جریان القایی از سیم در یک طرف به سیم مرکزی و سیم خارجی دیگر متفاوت خواهد بود: و . مقدار جریان القایی بین دو سیم بیرونی یکسان خواهد بود – و فازهای نسبی ثابت می مانند. اکنون می‌توانیم مجموع را رسم کرده و آرایش‌های مثلثی و خطی را با هم مقایسه کنیم.